BFS algorithm

一些最近遇到的广度搜索算法题

几道广度搜索算法

最近在看算法然后就看见了几道BFS的算法题，之前对于算法学的并不好，基本全忘了，正好用着复习一下

方块问题

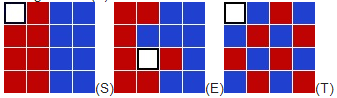
在一个4行4列的平面立面，有7个红色块8个蓝色块和一个白色块，你只能移动白色的快，当移动后，白色块会和被移动的块交换位置。
使用上下左右来记录白色块的交换顺序，问：最少需要多少步能让图形从S变为T

分析：一开始看见这个题目是没有什么思路的，看了提示用BFS,然后采取把BFS相关算法介绍看了一下，才大概有个思路，通过广度搜索暴力求解答案。
因为图比较小，所以花的时间并不是太多。简单的说就是模拟所有可能路径找到最短的那条。

def exchange(status, p1, p2):
    # 交换P1 P2，
    small=p1 if p1<p2 else p2
    big=p2 if p2>=p1 else p1
    return status[:small]+status[big]+status[small+1:big]+status[small]+status[big+1:]
  


def go(node):
    # path: 到达目前状态的路径
    # cursor: 可移动块所处的位置
    # status: 当前状态
    (path, cursor, status) = node
    if cursor == 0 and status == '2101101001011010':
        print(path)
    if status in visited:
        return
    visited[status] = True
    if cursor + 4 < 16: # go down
        patterns.append((path + "D", cursor + 4, exchange(status, cursor, cursor + 4)))
    if cursor - 4 > -1: # go up
        patterns.append((path + "U", cursor - 4, exchange(status, cursor, cursor - 4)))
    if cursor % 4 < 3: # go right
        patterns.append((path + "R", cursor + 1, exchange(status, cursor, cursor + 1)))
    if cursor % 4 > 0: # go left
        patterns.append((path + "L", cursor - 1, exchange(status, cursor, cursor - 1)))


patterns = [("", 0, '2011001100110011')]
visited = {} # 保存到达过的状态
count = 0
while (count < len(patterns)):
    if go(patterns[count]):
        break
    count += 1

当然如果用位运算应该效率更高，不过因为不擅长位运算就不用位运算了。

二叉树宽度

定义二叉树的宽度为二叉树中包含节点最多的层中的节点数。现有一颗二叉树，其深度不大于 N
基本结构为
typedef struct tree
{
struct tree left;
struct tree right;
} * Btree
求二叉树宽度， ROOT 为此二叉树根节点指针

分析：BFS简单的概念题，二叉树搜索，循环遍历每一层的节点，计算出个数，输出一个最大值即可

class Node:
    def __init__(self):
        self.left = None
        self.right = None

def max_width(root):
    if not root:
        return 0
    arr1 = []
    arr2 = []
    arr1.append(root)
    ans = 1
    while len(arr1) > 0:
        arr2 = []
        for node in arr1:
            if node.left:
                arr2.append(node.left)
            if node.right:
                arr2.append(node.right)
        ans = max(ans, len(arr2))
        arr1 = arr2
    return ans

n1 = Node()
n2 = Node()
n3 = Node()
n4 = Node()
n5 = Node()
n6 = Node()
n7 = Node()
n8 = Node()
n9 = Node()
n0 = Node()
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
n4.right = n6
n5.left = n7
n5.right = n8
n3.right = n9
n3.left = n0
print max_width(n1)
print max_width(n2)

和BFS无关的一道题

搜狐员工小王最近利用假期在外地旅游，在某个小镇碰到一个马戏团表演，精彩的表演结束后发现团长正和大伙在帐篷前激烈讨论，小王打听了下了解到， 马戏团正打算出一个新节目“最高罗汉塔”，即马戏团员叠罗汉表演。考虑到安全因素，要求叠罗汉过程中，站在某个人肩上的人应该既比自己矮又比自己瘦，或相等。 团长想要本次节目中的罗汉塔叠的最高，由于人数众多，正在头疼如何安排人员的问题。小王觉得这个问题很简单，于是统计了参与最高罗汉塔表演的所有团员的身高体重，并且很快找到叠最高罗汉塔的人员序列。 现在你手上也拿到了这样一份身高体重表，请找出可以叠出的最高罗汉塔的高度，这份表中马戏团员依次编号为1到N。
输入描述:
首先一个正整数N，表示人员个数。
之后N行，每行三个数，分别对应马戏团员编号，体重和身高。
输出描述:
正整数m，表示罗汉塔的高度。
输入例子:
6
1 65 100
2 75 80
3 80 100
4 60 95
5 82 101
6 81 70
输出例子:
4

分析：这个题目我觉得挺有趣的，主要是身高体重2列，排序好身高然后就需要比较体重。搜了一下发现是一个最长上升子序列长度的问题。现在的问题就变成了找体重的最长子序列就可以了。
最长子序列可以开一个栈，每次取栈顶元素top和读到的temp元素做比较，如果temp>top就把temp入栈，如果temp<top就二分查找栈中比temp大的第一个数并用temp替换它。最长子序列即为栈的大小。参考

def lcs(nums):
    stack=[]
    stack.append(-1)
    top=0
    for i in range(len(nums)):
        print(stack)
        if nums[i]>stack[top]:
            stack.append(nums[i])
            top+=1
        else:
            low=1
            high=top
            mid=0
            while low<=high:
                mid=(low+high)//2
                if nums[i]>stack[mid]:
                    low=mid+1
                else:
                    high=mid-1
            stack[low]=nums[i]
            
    print(top)
    print(stack[1:])
    return

lcs([1,5,2,3,7,22,11,20])